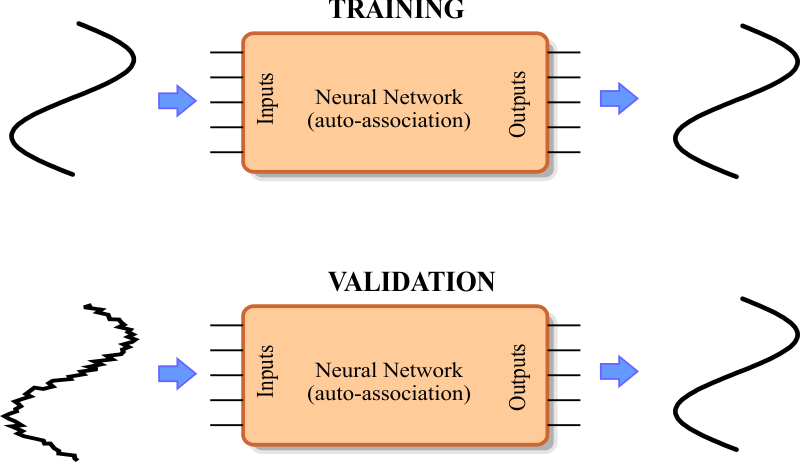
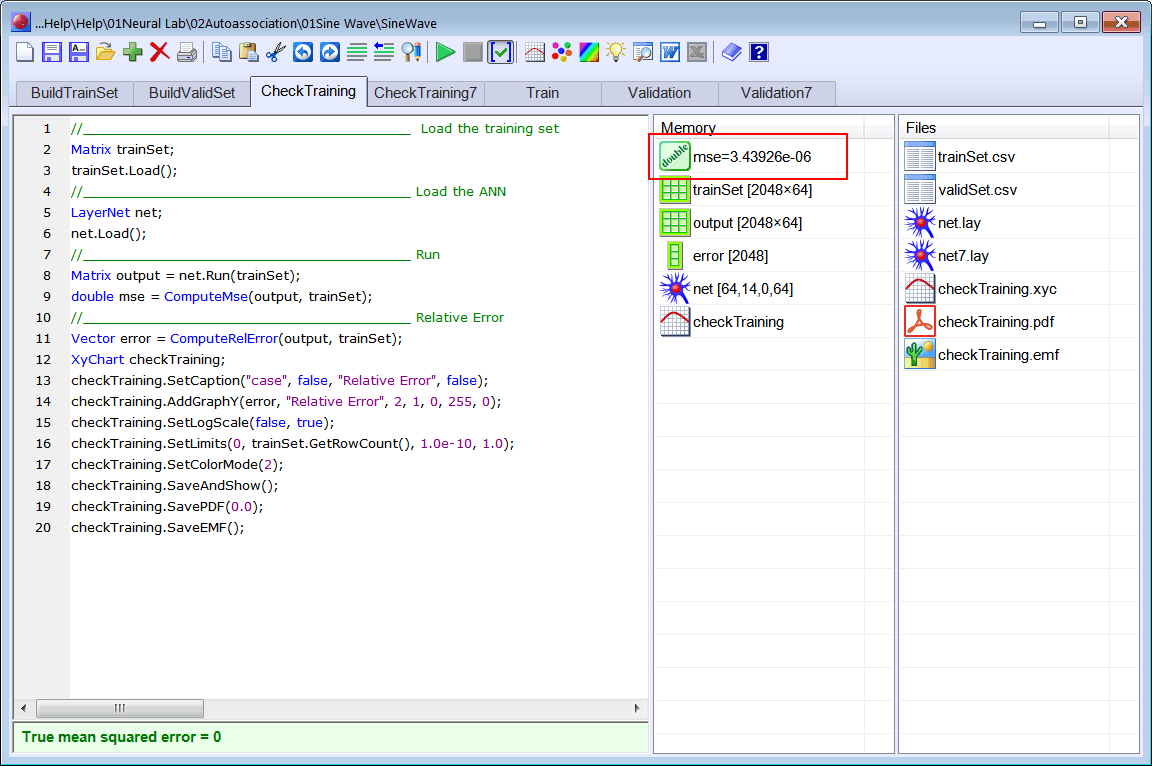
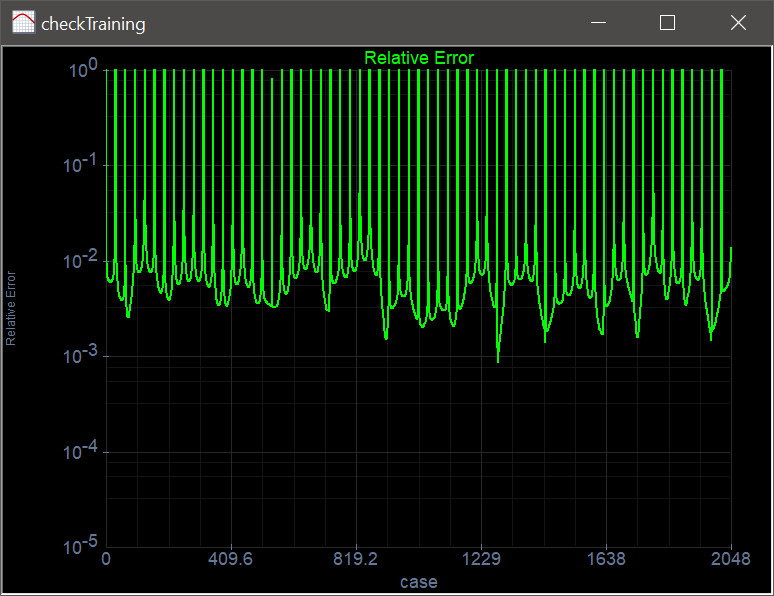
int numInputs = 64;
int i;
//_________________________ Network Setup
LayerNet net;
net.Create(numInputs, 7, 0, numInputs);
for(i = 0; i<numInputs; i++)
{
net.SetInScaler(i, -1.0, 1.0); // Input values are from -1.0 to 1.0
net.SetOutScaler(i, -1.0, 1.0); // Output values are from -1.0 to 1.0
}
//________________________ Load and set the training set
Matrix trainSet;
trainSet.Load();
net.SetTrainSet(trainSet, trainSet, false);
//________________________ Train
net.TrainSimAnneal(100, 100, 15, 0.01, false, 4, 1.0e-12);
net.TrainConjGrad(1000,1.0e-12);
//_____________________________ Save the trained network
net.Save();
|
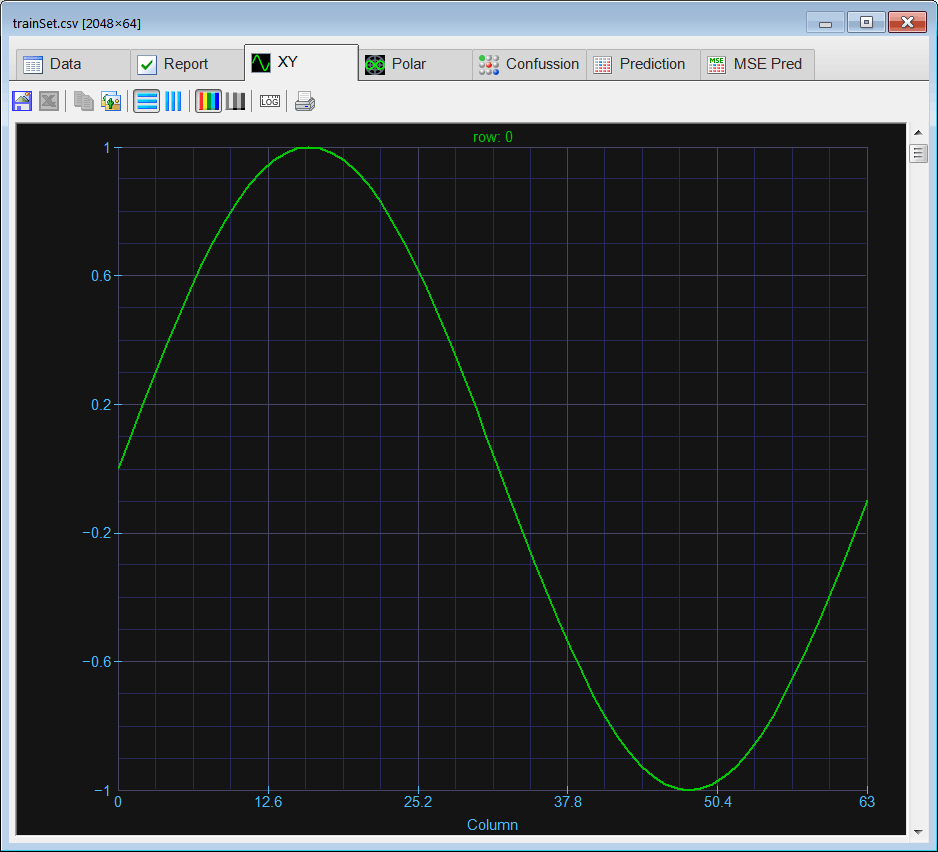
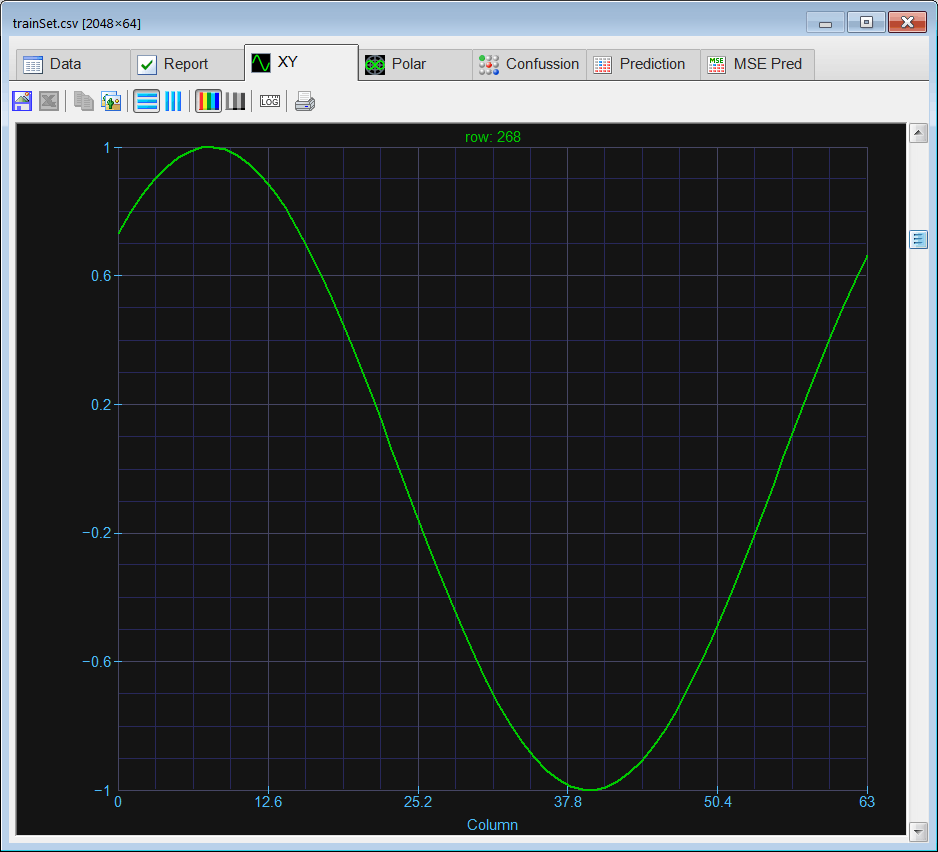
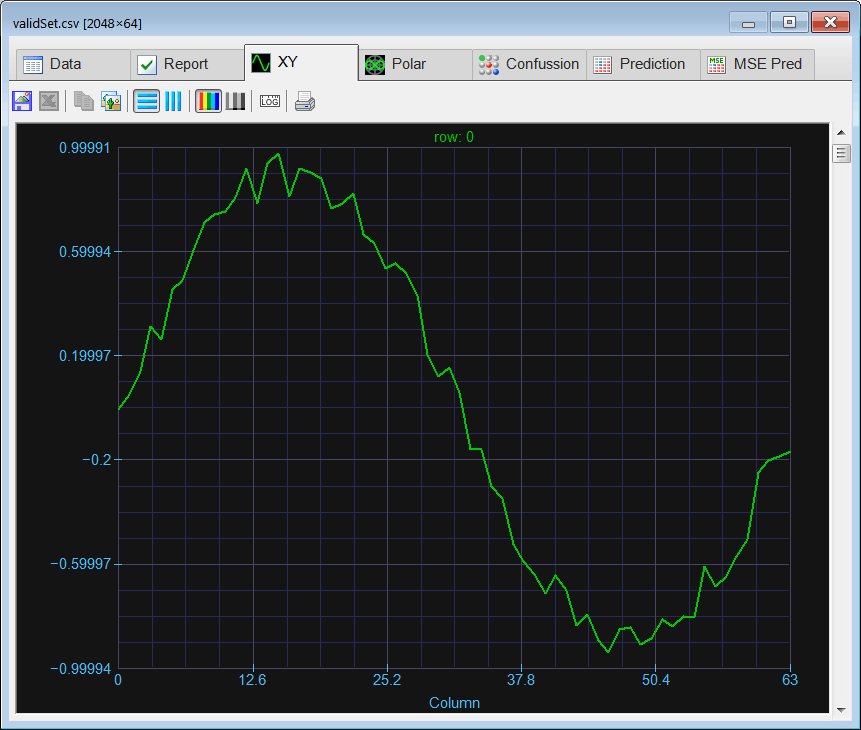
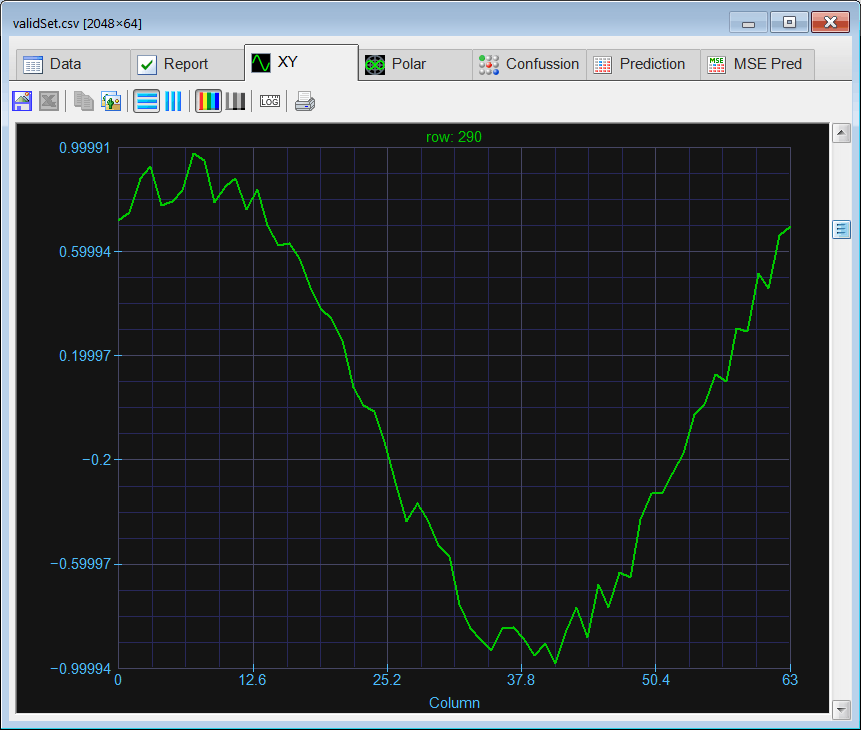
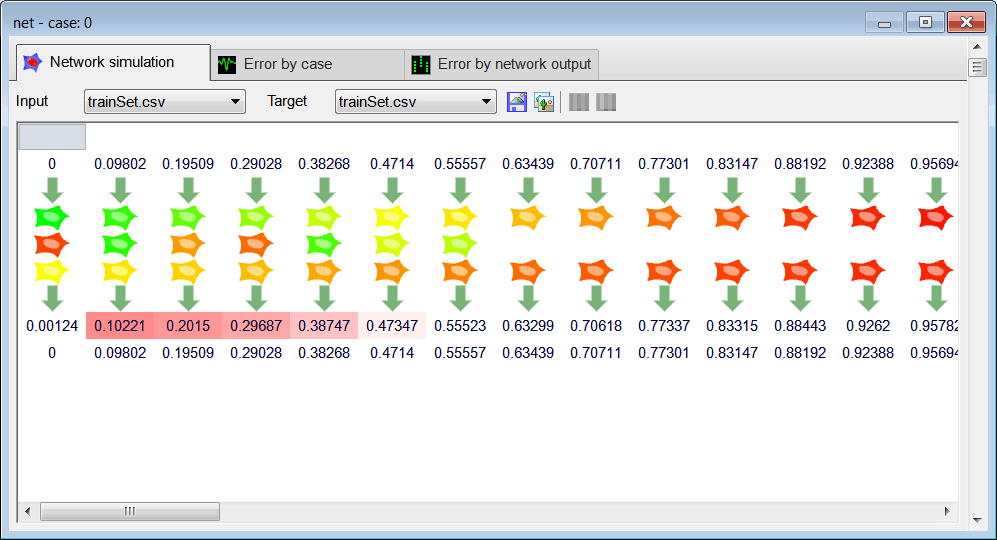
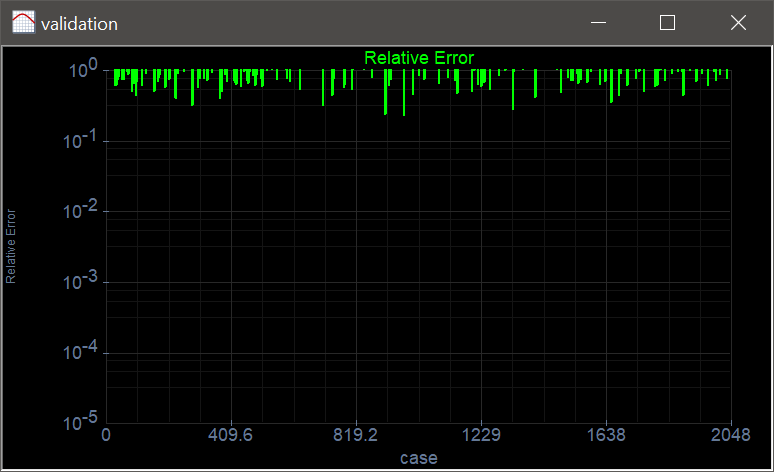
 Run click the button to execute the code. If you do not have any errors, the training set will be generated and displayed on the variable list and the file list. Click on the file to see its contents. Use the scroll bar at the right to visualize each training case. Each case should be a sine wave at a different phase. Observe that in this specific case the training set input and target are the same.
Run click the button to execute the code. If you do not have any errors, the training set will be generated and displayed on the variable list and the file list. Click on the file to see its contents. Use the scroll bar at the right to visualize each training case. Each case should be a sine wave at a different phase. Observe that in this specific case the training set input and target are the same.